You need to do a lot of maths to point at the Moon. You might think it’s a simple orbit and there should be a simple way to calculate the Moon’s position based on the current time, and you’d be generally right except for the word “simple”. Let’s start by breaking this down into stages:
- Find the Moon’s orbital parameters
- Calculate its position in cartesian (x, y, z) coordinates
- Transform those coordinates according to the Earth’s rotation
- Find your own location in cartesian coordinates
- Calculate the direction to point in
But before we can do any of that we need to decide on some reference frames.
I’m going to include code links to the Cosmic Signpost in each section.
Reference Frames
Code link: reference_frame.h
In astronomy there are several different reference frames you can use. The most common are:
- International Celestial Reference Frame (ICRF): the celestial reference frame, centred at the centre of our solar system and fixed with regards to several distant star systems.
- International Terrestrial Reference Frame (ITRF): the terrestrial reference frame, which is centred at the centre of the earth, and rotates with it.
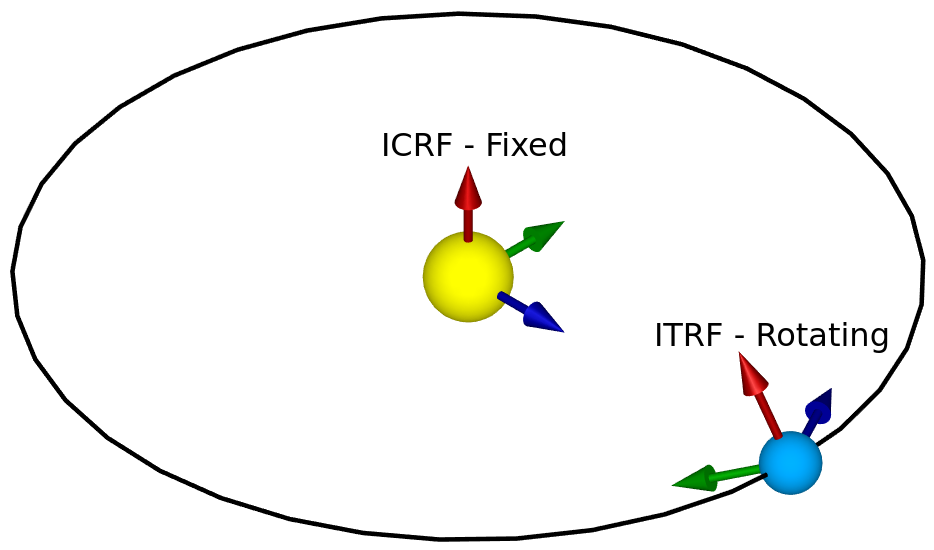
Tracking things in space from the surface of Earth often requires converting between these two frames. However, a frame centred on the Sun like ICRF isn’t necessary for tracking the Moon – for that we need an Earth Centred Inertial (ECI) frame (which is centred on Earth but doesn’t rotate with it) in addition to ITRF.
First, to convert between ITRF and ECI we need to define our axes. We’ll be using a cartesian coordinate system called Earth Centred, Earth Fixed (ECEF) for ITRF, and something very similar but non-rotating for ECI. In ECEF, (0, 0, 0) is at the centre of the Earth, the Z axis points towards the north pole, the X axis points towards the point where the prime meridian touches the equator (GPS 0, 0), and the Y axis points 90 degrees east of that.
There are several steps to the conversion between ITRF and ECI, but because ITRF is rotating and ECI isn’t, we need to know the precise time whenever we convert between them. There’s a reference time called J2000, and we know the exact angles between the two frames at that exact time. From there we can use the speed of the Earth’s rotation (and other things) to figure out what the angles are at any particular time.
Unfortunately, the definition of our reference time J2000 is already quite confusing: it was originally defined as midday (not midnight, because astronomers observe at night) on the 1st of January in the year 2000. However, this was defined in Terrestrial Time, which (a) is an ideal that can’t be measured by real clocks, and (b) differs from UTC by around 32.184 seconds, so the actual value of J2000 is 11:58:55.816 UTC on the 1st of January, 2000. It’s worth noting that at the time of writing we have had 5 leap seconds since J2000 – not accounting for those could throw the calculations off, as leap seconds are designed to keep UTC in sync with the Earth’s rotation.
Next, let’s clarify which ECI we mean, because so far we’ve only said it’s an inertial frame centred at the centre of the Earth, not where the axes are. We have two planes we could use: the equatorial plane (which forms Earth’s equator) in the orientation that it was in at the moment of J2000, and the ecliptic plane (which the Earth orbits the Sun in), they differ by around 23.4° because of Earth’s axial tilt. Since the orbits of all of the planets and the Moon are usually defined in terms of the ecliptic plane, we’ll use that. We’ve decided that the Z axis points up from the ecliptic plane, and we can say that the Y axis is 90 degrees east of the X axis, but we still need to define the X axis. We can do this based on where the prime meridian was pointing at J2000, but the normal definition is actually based on where the mean vernal equinox was at J2000.
The vernal equinox happens in March every year, at the moment when the line that forms the intersection between the ecliptic and equatorial planes points directly towards the Sun. You’ll notice that this is in March, while J2000 is in January – the X axis is based on where the equinox line (i.e. that intersection of the two planes) is in January. The equatorial plane slightly changes over time because of slight variations in the Earth’s axis, which means the direction of the equinox line is constantly, but slowly, changing. Notice that since our X axis is along this line at J2000, we can perform a simple rotation around the X axis to compensate for the Earth’s axial tilt and convert between this ecliptic ECI frame (where the Z axis points upwards from the ecliptic plane) and an equatorial ECI frame (where the Z axis points towards the north pole).
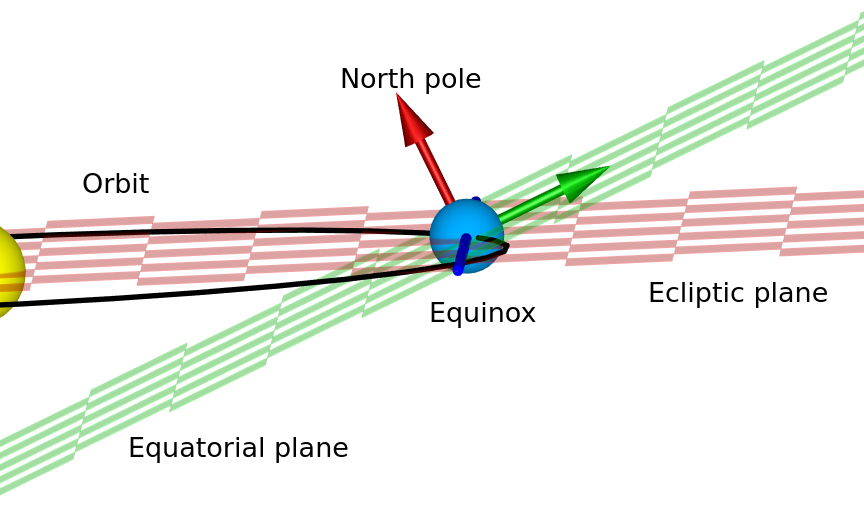
The equinox line (blue, defining the X axis) at a random point in the Earth’s orbit around the Sun. The date in this diagram doesn’t coincide with the date of the equinox (when days and nights have an equal length), because the line is not currently pointing at the Sun.
Now that we have some reference frames defined, we can start to use them.
Finding the Moon’s Orbital Parameters
Code link: moon_orbit.cc
You might have heard that the Moon is very slowly drifting away from Earth at the rate of a few centimetres per year. This is only one of the ways that the parameters of its orbit are changing: it is constantly affected by its orbit around the Earth (which moves it closer to and further away from the Sun), the Earth’s orbit around the Sun, and potentially other things too.
The Keplerian Orbital Parameters are six numbers that can exactly define an elliptical orbit of one body around another. They are:
- Semi-major axis: the radius of the orbit at its widest point
- Eccentricity: the scale of how elliptical the orbital ellipse is (0 meaning circular, 1 and over meaning that it’s not orbiting any more)
- Inclination: the angle of the orbital plane with respect to some reference frame (in our case, the ecliptic ECI frame)
- Longitude of Ascending Node: the angle around the thing we’re orbiting (from some reference direction) where we measure the inclination from. Specifically, this is the angle where the Moon moves from below the Ecliptic plane to above it.
- Argument of Periapsis: the angle around the orbit from the Longitude of Ascending Node where the two bodies are closest to each other.
- Mean Anomaly: the current angle of the smaller body around the larger one, if you assume that the orbit is circular and the smaller body is moving at a constant speed around the larger one. (This is useful because it generally increases uniformly over time, and it can be used to calculate other parameters called the Eccentric Anomaly and True Anomaly, which are actual angles around the orbit).
For a much more in-depth and interactive explanation of how these 6 parameters work together see this page: https://ciechanow.ski/gps/#orbits – it’s geared towards explaining in detail how GPS works, but as part of that it goes into detail on all of the orbital parameters.
For the Moon, all six of these parameters vary over time. The best data source I could find for this was the JPL Horizons tool, which allows you to choose any body in the solar system and get a table that includes more than just these parameters for any range of dates/times.
To begin with, I downloaded all of the Moon’s orbital parameters at a daily resolution for 16384 days starting at midnight on the 1st of January 2000 (unfortunately, due to the way the data is exported, all of the dates were offset by -0.5 days from J2000, but this is correctable).
To analyse this large dataset, I wrote some code in Python to display graphs and do some numeric analysis. The first part of this was to perform a Fast Fourier Transform (FFT) to see which frequencies each component oscillates at. I manually gathered the top 8 frequency components from the graph of each FFT, since the aim is to find a good approximation rather than storing all of this data. For the semi-major axis, eccentricity, and inclination, just an FFT was enough. But the longitude of ascending node, argument of periapsis, and mean anomaly all have linear components too (i.e. the angle has a cumulative increase/decrease as well as oscillations), and their angles always wrap around when they get to 360°. To correct for this, I used a function in scipy called unwrap() with the period set to 360, which turns a time series like the one on the left into the one on the right.
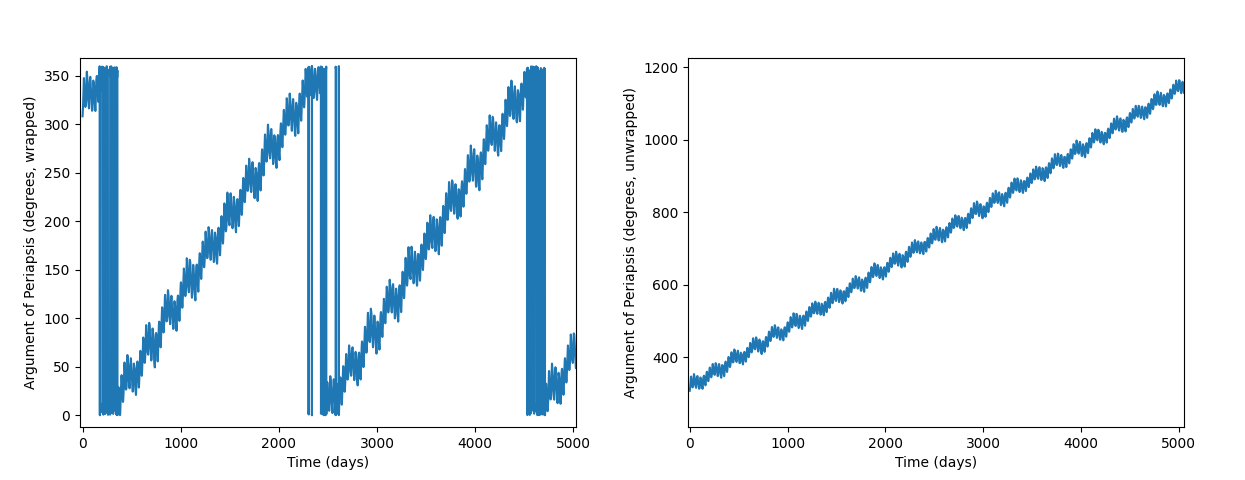
And because this still has a linear component, I first approximated the linear gradient and subtracted it out before performing the FFT. From there, all six graphs look similar, although each have different oscillations.
Finding the initial frequencies was as simple as looking them up in the FFT graphs: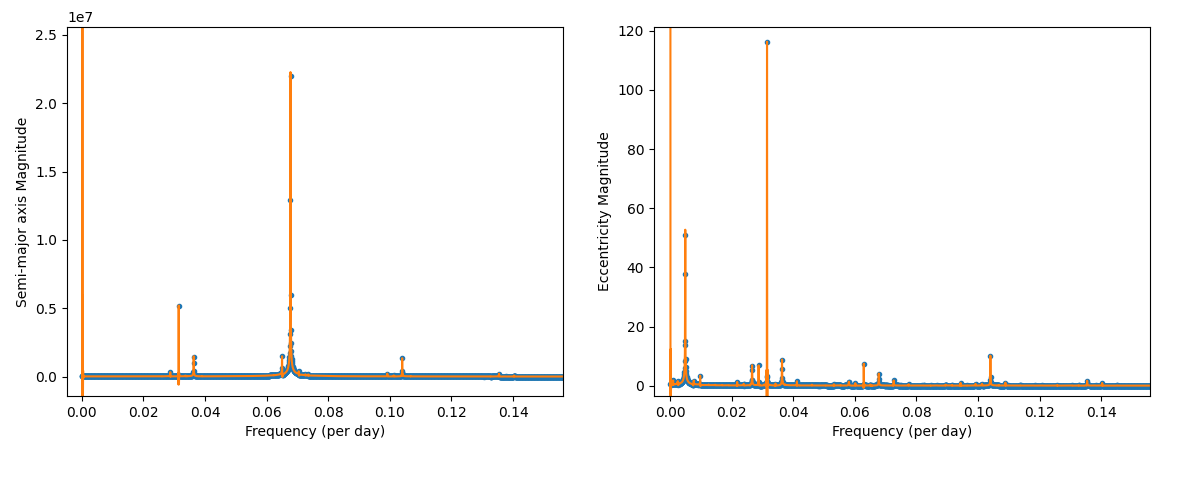
Next, I used a function similar to the following to define the curve-fitting process:
$$a_t = \sum_{i=1}^{8} (S_i sin(2 \pi F_i t) + C_i cos(2 \pi F_i t))$$
Where $a_t$ is the semi-major axis at time $t$, $F_i$ represents one of the eight frequency components (I chose 8 as an arbitrary trade-off between accuracy and complexity), and $S_i$ and $C_i$ are sine and cosine amplitudes. The parameters to optimise are $F_i$, $S_i$, and $C_i$. Using sine and cosine amplitudes is equivalent to using a magnitude and a phase, but it gives each of the parameters a differentiable effect on the output, which makes it easier to optimise than a phase angle. It’s possible to turn the sine and cosine amplitudes into magnitude and phase using the following transformation (example in desmos):
$$magnitude = sqrt(S^2 + C^2)$$
$$phase = atan2(C, S)$$
Functions like the one for $a_t$ above, with some additions for dealing with constant and linear components, were used as the input to scipy.optimize.curve_fit() to find the final parameters, which consist of:
- Eight frequency components, for each of the six parameters.
- Eight sine and eight cosine amplitudes, for each of the six parameters, which we use to calculate the magnitudes and phases using the formulae above.
- A constant offset for each of the six parameters.
- A linear time-multiplier for the Longitude of Ascending Node, Argument of Periapsis, and Mean Anomaly parameters.
We have now optimised these six functions on 16384 days (or just over 44 years) of data from 2000 to 2044. Testing it on the next 16384 days of data from JPL Horizons showed that it fits reasonably well. From there, we can calculate with reasonable accuracy the orbital parameters of the Moon at any point in at least the next ~70 years, but likely much longer.
Keplerian Orbits
Code link: keplerian_orbit.cc
So, how do we use these six orbital elements to calculate the position of the Moon? This is heavily based on NASA’s documentation here about finding the approximate positions of planets, but it applies to any Keplerian orbit including the Moon’s (if you have accurate orbital elements).
First, we need to find the x and y positions in the Moon’s orbital plane, and for that we need to find the Eccentric Anomaly ($E$) from the Mean Anomaly ($M$) and the Eccentricity ($e$):
$$M = E\ -\ e \cdot sin(E)$$
It’s not possible to solve this numerically for $E$, but we can approximate it using Newton’s method. We’re trying to find $M\ -\ E + e \cdot sin(E) = 0$, so let’s set:
$$F(E) = M\ -\ E + e \cdot sin(E)$$
$$E_0 = M\ -\ e \cdot sin(M)$$
(I suppose setting $E_0 = M$ might work too.) Then we can iterate this:
$$F'(E) = -1 + e \cdot cos(E)$$
$$E_{n+1} = E_n\ -\ F(E_n) / F'(E_n)$$
Repeating this until the delta ($F(E_n) / F'(E_n)$) is small enough gives us a good approximation of $E$. Then, we can use the eccentric anomaly $E$, the eccentricity $e$, and the semi-major axis $a$ to get $x$ and $y$, and our $z$ starts at the origin:
$$x = a (cos(E)\ -\ e)$$
$$y = a \sqrt{1\ -\ e^2} \cdot sin(E)$$
$$P_{initial} = (x, y, 0)$$
From there, we just need to rotate these coordinates into position. In my implementation, I used quaternions (extremely useful tutorial here) for this because they are a nicer way of representing arbitrary rotations and they’re easier to read than complex matrix multiplications. However, for simplicity below I’ve assumed an equivalent rotation matrix for each step:
$$P_{periapsis} = R_Z(argument\ of\ periapsis) \times P_{initial}$$
$$P_{inclined} = R_X(inclination) \times P_{periapsis}$$
$$P_{final} = R_Z(longitude\ of\ ascending\ node) \times P_{inclined}$$
This gives us $P_{final}$ as the cartesian position in our reference frame, in this case the ecliptic plane centred on the Earth.
Earth’s Rotation
Code links: earth_rotation.cc, and some of cartesian_location.cc
We can calculate the Moon’s position in ECI, but we need it in ECEF. The next step is to convert between them. There are several steps here:
- Convert from Ecliptic ECI to J2000-Equatorial ECI (based on the J2000 north pole and equator), by applying the axial tilt.
- Convert from J2000-Equatorial ECI to the ECI frame based on the current north pole and equator, this is known as CEP or “Celestial Ephemeris Pole”. This involves applying axial precession and nutation.
- Convert from this CEP frame to ECEF, by applying the rotation of the Earth.
The ESA provides a full description of the steps on their Navipedia site, but it provides a lot of technical detail without much context, so I’ll just summarise here.
Step 1 is very simple, since we defined our ecliptic and equatorial planes with the X axis pointing along the line where they intersect, we can just rotate the coordinates by 23.4° on the X axis.
Step 2 is more complicated. The north pole (and therefore the equator) actually move around over time, in cycles on various different time scales. The largest movement is from axial precession, which means that over 26,000 years the Earth’s axis makes one full rotation. This actually means that in 13,000 years, the northern hemisphere will have summer in January and winter in July. It also means that the vernal equinox line by which we define the ECI X axis moves over time, doing a full circuit in 26,000 years.
The other part of step 2, Nutation, is higher-frequency than precession, and it occurs because the forces that lead to precession are not constant, but vary over the course of the Earth’s orbit due to gravity from the Sun, Moon, and planets. Applying it correctly involves using some long lookup-tables.
Step 3 is mostly about the rotation of the Earth on its (now well-defined) axis. There is also a component called Polar Motion, which is a slight drifting of the axis with respect to the Earth’s crust, but it has a tiny magnitude and requires frequent updates to calculate in an up-to-date way, so I’m ignoring it here.

Sidereal time diagram. Xaonon, CC BY-SA 4.0, via Wikimedia Commons.
The Earth rotates on its axis once every 23 hours, 56 minutes, and ~4 seconds. The difference between this and the 24 hours you might expect is because we need to measure the sidereal rotation (compared to ECI) rather than the rotation compared to the direction of the Sun from Earth, which is always changing. The extra 3 minutes and ~56 seconds add up over the course of a year to one extra sidereal rotation.
The details of this rotation on the ESA website are quite confusing. They define $\theta_G$ as the Greenwich Mean Sidereal Time (GMST), in terms of a fixed rotation over time compared to a reference $\theta_{G_0}$. The changing component is based on the current time in UT1 (which is very close to UTC), but they didn’t provide a reference epoch, so I initially assumed it was J2000, but in fact the reference is defined at midnight at the start of the current day. (In retrospect, they also say that $\theta_{G_0}$ is the GMST at $0^h$ UT1, but it wasn’t clear to me where they were counting hours from – what finally made me notice the error was that both $\theta_{G_0}$ and $\theta_G$ account for the sidereal rotation, and they’re added together in the end).
From $\theta_G$ (GMST), we need to correct for nutation again to get $\Theta_G$ (GAST, or Greenwich Apparent Sidereal Time), and then rotate the Earth by that angle. All of the rotation matrices on the ESA website are inverted (they rotate in the wrong direction), and all of the angles passed in to them are negated to compensate. Converting this all to use standardised quaternions for rotation made things much easier to understand.
Finding our own location
Code link: location.cc
To be able to point at some ECEF coordinates, we first need to know where we are. GPS coordinates are polar coordinates, which give a latitude (the angle away from the equator), a longitude (the angle away from the prime meridian), and an elevation (the height above the Earth’s reference ellipsoid).
The ellipsoid can be defined in terms of a polar radius (from the north or south pole to the centre) and an equatorial radius (from the equator to the centre). Obviously the Earth’s height varies much more than a perfectly smooth ellipse, and even sea level doesn’t quite match the ellipsoid. GPS receivers usually give you both an elevation above mean sea level and an elevation above the reference ellipsoid.
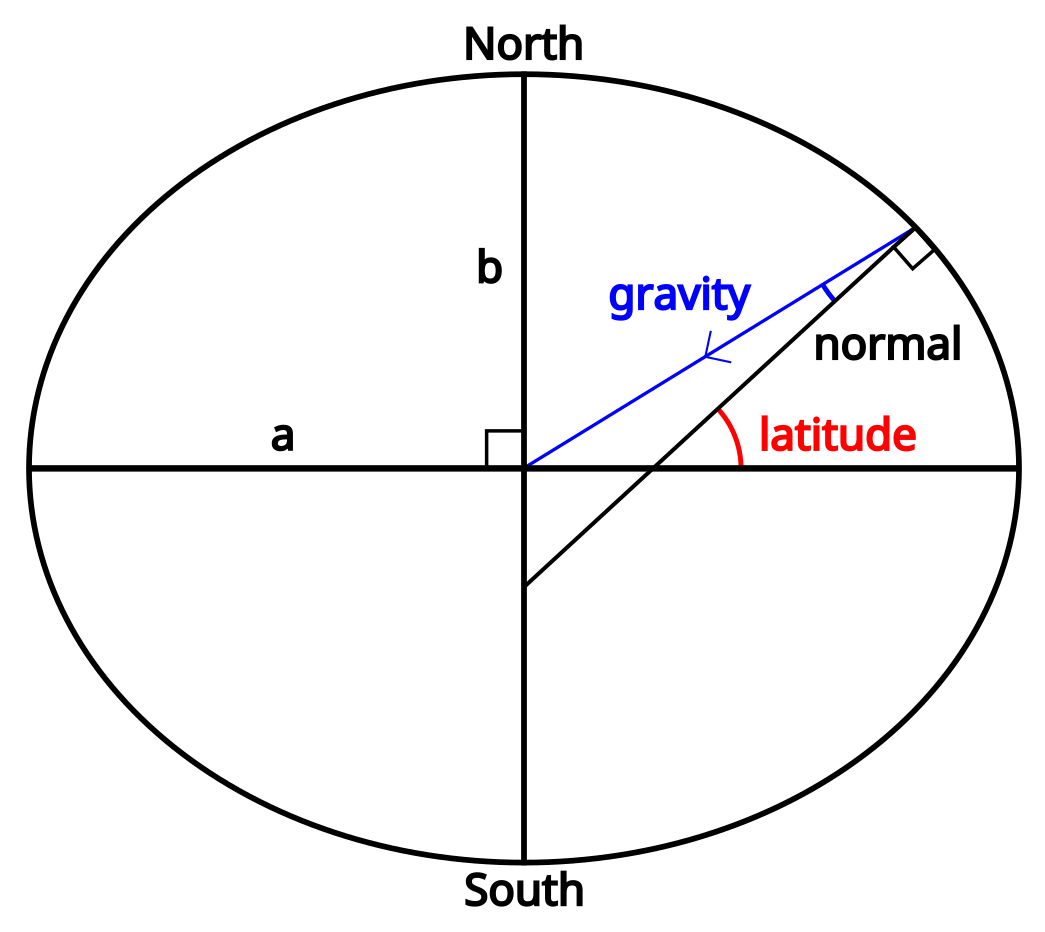 To begin with, it’s worth noting that because we’re not standing on a sphere, a line pointing at a normal to the surface (one of the definitions of “straight down”) doesn’t necessarily point to the centre of the Earth. It’s close, and it does intersect the line going from the north pole to the south pole, but unless we’re actually standing on the equator or the north pole it won’t pass through the exact centre.
To begin with, it’s worth noting that because we’re not standing on a sphere, a line pointing at a normal to the surface (one of the definitions of “straight down”) doesn’t necessarily point to the centre of the Earth. It’s close, and it does intersect the line going from the north pole to the south pole, but unless we’re actually standing on the equator or the north pole it won’t pass through the exact centre.
The first number we need to calculate is the distance along the normal from our location to the line between the north and south poles. If we call the radius at the equator $a$ and the radius at the poles $b$, this can be calculated as:
$$N(lat) = \frac{a^2}{\sqrt{(a \cdot cos(lat))^2 + (b \cdot sin(lat))^2}}$$
From there, it’s relatively easy to find the $x$ and $y$ coordinates in ECEF:
$$x = (N(lat) + elevation) \cdot cos(lat) \cdot cos(long)$$
$$y = (N(lat) + elevation) \cdot cos(lat) \cdot sin(long)$$
Finding $z$ is slightly more complicated, but doesn’t depend on the longitude:
$$z = \left(\frac{b^2}{a^2} \cdot N(lat) + elevation\right) \cdot sin(lat)$$
Pointing
Code link: cartesian_location.cc (specifically, see directionTowards())
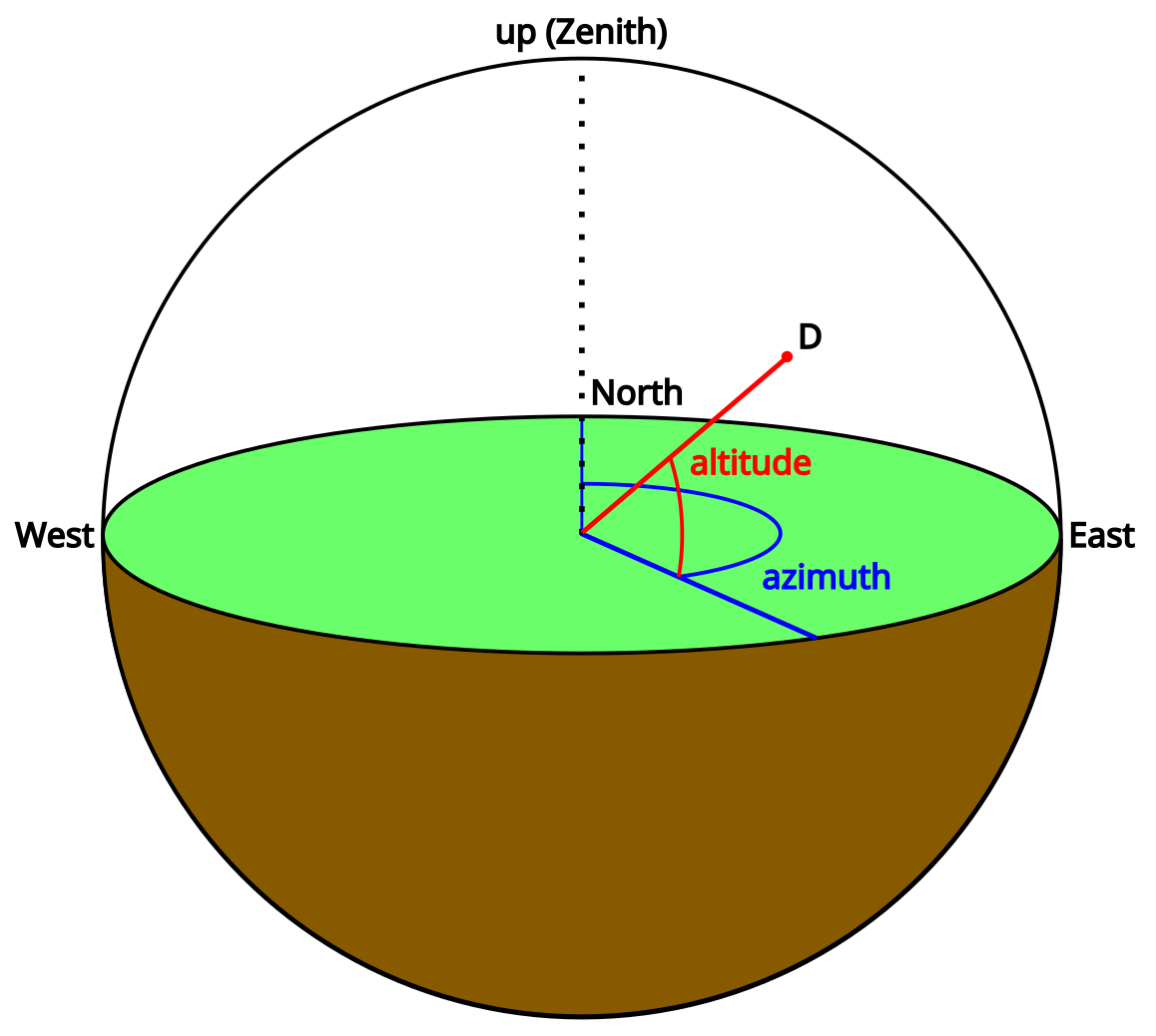 We have the coordinates of ourselves and the Moon, now we just need to point from one of them to the other. We can already calculate a vector, but it’s not very useful without some reference to compare it to. We need to know where that vector is pointing in a local coordinate system.
We have the coordinates of ourselves and the Moon, now we just need to point from one of them to the other. We can already calculate a vector, but it’s not very useful without some reference to compare it to. We need to know where that vector is pointing in a local coordinate system.
The two angles we need to point at something are often called the azimuth and the altitude. Note that the altitude here is an angle, and not the height above the ellipsoid that I’ve been calling elevation – it seems like in astronomy the term “altitude” is overloaded, and these two terms are often used interchangeably, so I’ve arbitrarily picked “elevation” for height and “altitude” for this angle.
If you’re standing on the surface of the Earth and pointing, your finger’s azimuth is the angle between north and the direction you are pointing (0° = north, 90° = east, etc.). Your finger’s altitude is the angle upwards from the horizon to it. Using these two angles, we can point towards any object in 3D space.
We need a reference direction: the normal to the surface of the Earth ellipsoid at our current location. This is fairly easy to define based on our latitude and longitude:
$$\vec{up} = \begin{bmatrix} x \cr y \cr z \end{bmatrix} = \begin{bmatrix} cos(lat) \cdot cos(long) \cr cos(lat) \cdot sin(long) \cr sin(lat) \end{bmatrix}$$
Getting the altitude from here is simple, given a direction to point $\vec{D}$:
$$altitude = 90\ -\ arccos(\vec{up} \cdot \vec{D})$$
Finding the azimuth is trickier – the easiest way I’ve found is to first rotate both $\vec{D}$ and $\vec{up}$ to the point where the prime meridian crosses the equator:
$$toPrimeMeridian = atan2(\vec{up}.y, \vec{up}.x)$$
The result from atan2() is the anticlockwise angle from the prime meridian, when viewed from the north pole. Our rotations are clockwise around the axis we choose, and we’re looking from the north pole to the south pole, so to remove this rotation we need to rotate clockwise around the negative Z axis:
$$\vec{up}_{prime\ meridian} = R_{-Z}(toPrimeMeridian) \times \vec{up}$$
Next, let’s put this at the equator. This time we’re looking along the positive Y axis:
$$toEquator = atan2(\vec{up}_{prime\ meridian}.z, \vec{up}_{prime\ meridian}.x)$$
$$\vec{up}_{0,0} = R_Y(toEquator) \times \vec{up}_{prime\ meridian}$$
But we aren’t really interested in $\vec{up}_{0,0}$, we already know which way it’s pointing. What we need are those same rotations applied to $\vec{D}$:
$$\vec{D}_{0,0} = R_Y(toEquator) \times R_{-Z}(toPrimeMeridian) \times \vec{D}$$
And finally we can find our azimuth (converting from anticlockwise from east, to clockwise from north):
$$azimuth = atan2(1, 0)\ -\ atan2(\vec{D}_{0,0}.z, \vec{D}_{0,0}.y)$$
Using the azimuth and altitude together, we can figure out which direction to point in, and all we need as references are an up/down vector, and the direction of north. Putting all of this together, we can point at the Moon!
See https://github.com/abryant/CosmicSignpost for the code. There may be more blog posts coming about the motor control code, electronics, and hardware.
Thanks go to my partner Dalia, who pointed me towards scipy and specifically the unwrap function, and helped with analysing the FFTs of the Moon’s orbital elements.
Thanks also go to my Dad, who showed me how to use sine and cosine amplitudes as a more optimisation-friendly formula for the orbital elements than magnitude and phase.