My post on Moon Tracking covers most of the complexities involved in tracking things, but not quite everything. I chose to talk about the Moon first because it covered all of the most complex parts of the tracker. This post covers all of the rest of the things that the Cosmic Signpost can currently track.

Planets

Tracking planets in our solar system is only a small addition to the complexity of tracking the Moon.

JPL provides some approximate orbital parameters for tracking planets. They’re fairly simple models, so won’t be particularly accurate, but they’ve very simple to implement and given the distance from Earth the inaccuracies won’t be very noticeable.

However, they are all based on a heliocentric inertial reference frame. We have our ECI frame though, and the axes are in the same directions, so we should be able to subtract out the Earth’s position vector to get to that frame, right?

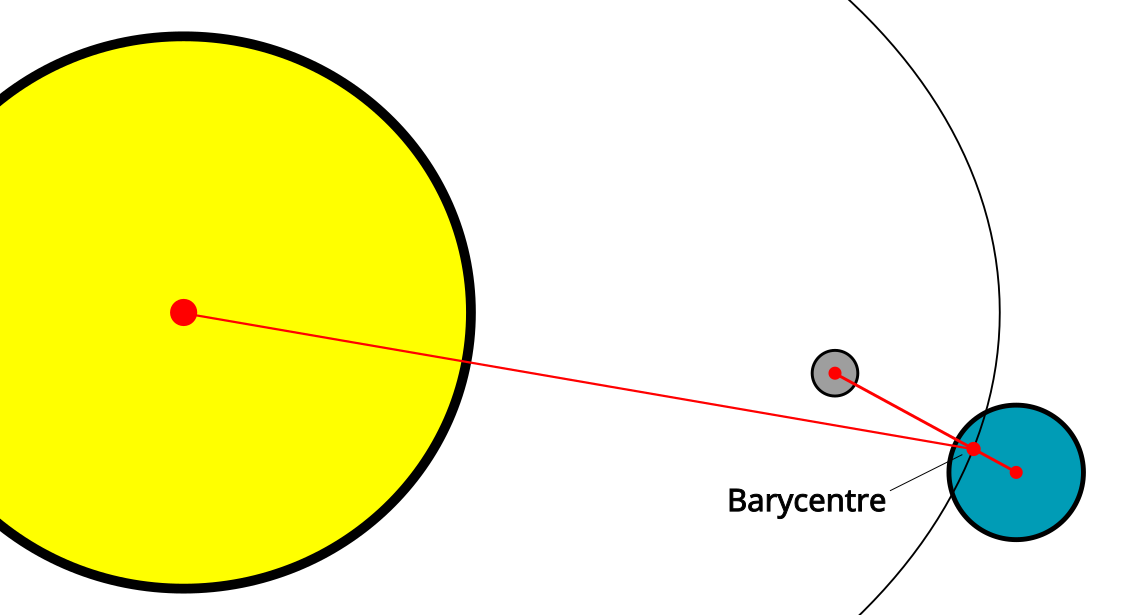
Unfortunately, the orbital parameters that JPL gives for Earth are actually the Earth-Moon-Barycentre. The Barycentre of a set of objects is the centre of mass of all of them together, and in the case of the Earth-Moon system, the Barycentre is about 4,671 km from the centre of the Earth, or most of the distance from the centre of the Earth to the crust. Since we already know how to track the Moon, we can track the Earth-Moon-Barycentre by multiplying the Moon’s position vector (from Earth) by the ratio of the Moon’s mass to the Earth’s mass, which is 7.349×10²² / (5.972×10²⁴ + 7.349×10²²) = 0.0121561693.

If we take the position vector from Earth to the Barycentre (which we can calculate from our Moon tracking as above), and subtract the position vector from the Sun to the Barycentre (which we can calculate based on JPL’s approximate planet positions), this will give us the Sun’s position in ECI. We can then add any heliocentric coordinates we like, and they will be in ECI, so now we can track the Sun and all of the Planets.

Distant stars

Distant stars (and galaxies, and whatever else is normally fixed in relation to the stars) are tracked using a Right Ascension and Declination. These are basically polar coordinates like latitudes and longitudes, but projected into the night sky. (In this analogy, the right ascension is the longitude, and the declination is the latitude).

We do know the distance of some stars, but it’s not always well documented and they’re so far away anyway that it shouldn’t really make a difference for tracking, so the simple (but slightly hacky) way to turn them into cartesian locations is to choose a distance that’s really far away, and make them all that distance from the Earth. I chose 10^100 m (which is ~10^84 light-years) for my range, because it’s a nice middle ground between being excessively far away and not overflowing a double-precision floating point number during calculations (they have a maximum value of 1.79×10^308).

These coordinates use the equatorial version of ECI discussed in the Moon Tracking post, so converting them to fixed coordinates just involves rotating the Earth as specified there. The Cosmic Signpost menu has list of interesting stars hardcoded into it, but you can also enter a Right Ascension and Declination manually and track that.

GPS Coordinates

These are the simplest to track, since we already have the code to convert from Latitude and Longitude to ECEF and we don’t even need to rotate the Earth. There’s not much to say here except that I’ve hardcoded a list of cities and other places that the Cosmic Signpost can track, and you can also enter a location manually using Latitude and Longitude coordinates (just like you can using Right Ascension and Declination for distant stars).

Earth’s Satellites

We’ve launched thousands of satellites into orbit around Earth over the last 70ish years, and there are standardised ways to track them that are quite accurate. The most well-known algorithm for this is called SGP4, and it factors in lots of things like the changing gravity from Earth, the Sun, and the Moon as well as the pressure of radiation coming from the Sun. It’s a very complicated algorithm that can be quite difficult to understand.

NORAD (which does most of this tracking) shares its data about the current orbits of satellites with CelesTrak.org, a non-profit that makes the data available publicly. CelesTrak has an API that can produce this data in multiple formats. The older format is the TLE (Two-Line Element Set), but it is annoying to parse and not future-proof (dates all have two-digit years, and the number of satellites that can be tracked is limited). The newer format is the Orbital Mean-Elements Message (OMM), which can be encoded in JSON, XML, or whatever is most convenient. CelesTrak provides an API for producing OMM messages that we can query by NORAD catalog number to look up any satellite that they provide data for. Here’s the International Space Station’s tracking information in JSON.

It’s important to note that the tracking data that CelesTrak provides is only useful if you use the SGP4 orbital propagation algorithm to find where a satellite is at a particular time. The orbital elements they provide won’t be accurate with any other algorithm. (There is also SDP4, which is a variation on SGP4 for satellites that are deeper in space, I’m referring to both algorithms as SGP4 here because the reference implementation switches between the two automatically.)

The most well-known implementation of SGP4 is by David Vallado, which he wrote as a companion to his book “Fundamentals of Astrodynamic and Applications”. His code is available via CelesTrak here.

Unfortunately, to a software engineer who is not an astronomer, the code is very difficult to read – most variables and functions have incomprehensible names, some of those variables are never actually used, and tens of variables at a time are often passed to sub-functions either by value or by reference without any explanation of why they’re passed that way. The parsing of TLEs is very coupled to the tracking, and there is no parser for OMM messages.

Partly because of some of these shortcomings, and partly in an effort to understand it better, I adapted this code to create my own version of the SGP4 propagator here (although I wouldn’t call it much of an improvement, because I still don’t fully understand the algorithm myself): https://github.com/abryant/CosmicSignpost/blob/main/lib/tracking/sgp4_propagator.cc

By giving the propagator a set of orbital elements and a time, we can get the current position of any trackable satellite in an equatorial ECI frame. The original aim of the Cosmic Signpost was to track the International Space Station, so by giving it NORAD Catalog Number 25544 we’ve accomplished that.

Things it can’t track (yet)

There are a few things that it would be possible to track in theory, but that I haven’t implemented in the Cosmic Signpost yet:

• Asteroids
• Comets
• Moons of other planets (it’s easier to just track the planet itself)
• Objects that are flying through our solar system without orbiting
• Aeroplanes
• Boats
• GPS trackers that share their location

I’d be happy to accept pull requests for these, if anyone feels like implementing them.